AlphaGo

In 2016, an AI system named AlphaGo stunned the world by defeating Lee Sedol, one of the strongest Go players in modern history. At the time, this milestone was considered at least a decade ahead of what most experts believed possible. How did AlphaGo manage this feat in a game renowned for its exponential complexity? The breakthrough came through combining established ideas in supervised learning, reinforcement learning, and search. Below, we peel back each layer of technology - showing precisely how AlphaGo went from raw data all the way to superhuman play.

Go: The Challenges and the Opportunity

To appreciate AlphaGo's approach, it is useful to understand the problem's scale. Go is played on a $19 \times 19$ board, giving it roughly $2.1 \times 10^{170}$ possible positions - far more than there are atoms in the observable universe. Classical search-based AI methods (like those used in chess programs prior to the 2010s) struggle with such a large branching factor. Traditional heuristics from chess, checkers, or shogi prove insufficient due to Go's more nebulous definitions of "local territory" and "global influence."

For decades, computer Go lagged far behind professional human play. Then came new advances in deep learning - particularly convolutional neural networks - combined with advanced reinforcement learning. Enter AlphaGo.

Key Components of AlphaGo

AlphaGo's final pipeline integrates four major pieces:

• SL Policy Network - A deep CNN that learns to imitate professional (human) moves.
• Rollout Policy - A simpler, fast policy used for thousands of quick simulations.
• RL Policy Network - An advanced policy refined by self-play reinforcement learning.
• Value Network - A deep network that estimates how likely a particular board position is to lead to a win.

A Monte Carlo Tree Search (MCTS) orchestrates these components in real-time play, picking moves that both follow promising "policy" hints and exploit a learned evaluation (value function).

Supervised Learning (SL) Policy Network

Rationale and Data

Initially, AlphaGo trains a policy network (denoted $\sigma$) to mimic how professional players respond to typical board states. DeepMind collected roughly 30 million positions from human games. Each position was paired with the move that the expert actually played. The goal: learn a probability distribution over legal moves that matches the expert's choices.

Architecture

• Input: $19 \times 19 \times 48$ feature planes capturing board information, such as stone color, liberties, and possibly game history.
• Convolutional Stack: 12-13 layers of $3 \times 3$ or $5 \times 5$ filters with ReLU activations.
• Output Layer: A $1 \times 1$ convolution with $192$ input channels and $1$ output channel, followed by a $19 \times 19$ softmax that assigns a probability to each board intersection.

In practice, this SL policy network can guess the human "expert move" with ~55-57% accuracy - already good enough to beat many strong amateurs.

Rollout Policy

Because simulating many games to completion can be too slow if we use a full deep network at every single move, AlphaGo also employs a rollout policy ($\pi$). This is a linear softmax classifier, much simpler than the deep policy net. Its benefits and drawbacks:

• Speed: It can generate a move in about 2 microseconds (μs), compared to about 3 milliseconds (ms) for the SL policy.
• Accuracy: Only ~24-25% at predicting human professional moves - far below the SL policy's 55%+.

Despite lower accuracy, it's absolutely vital in MCTS because it can handle the massive number of rollouts needed to explore future positions deeply.

Reinforcement Learning (RL) Policy Network

Imitating professional moves only gets you so far. To exceed typical professional level, AlphaGo must discover its own strategies. This is where reinforcement learning (RL) comes into play.

• Initialization

  The RL policy network starts as a copy of the SL policy network.

• Self-Play

  It then plays games against itself (or older versions of itself). By generating new positions and tracking win/loss outcomes, it gathers data well beyond the scope of the original human database.

• Policy Gradient Training

  After each self-play game:

  • If the RL policy eventually wins, it nudges the network parameters $\rho$ to make the chosen moves more likely next time.
  • If it loses, it does the opposite.

  Formally, this is akin to the REINFORCE algorithm: the reward $z$ is $+1$ for a win, $-1$ for a loss, and the gradient pushes the network to increase the probability of successful move sequences.

• Time & Resources

  Roughly one day on 50 GPUs was enough to achieve a sizable improvement, transforming the network into something that can consistently beat the original SL policy.

Value Network

Even with a refined policy, Go remains notoriously sensitive to small mistakes. A single misstep can lead to collapse in large-scale fights or endgames. Human players rely on "positional judgment" to gauge whether the current board is favorable. AlphaGo copies that via a Value Network - a deep CNN that outputs a single scalar in $[-1,+1]$, indicating how likely a board position is to lead to a final win.

Training the Value Network

• Self-Play Dataset: Using the (reinforced) RL policy network, AlphaGo plays millions of full games against itself. From each game, only one position is extracted so as not to correlate the entire move sequence. Each extracted position is labeled with the final game outcome.

• Architecture: Similar convolutional backbone as the policy net, but with:

  • Additional convolution layer(s),
  • A fully connected layer of around 256 units,
  • A single tanh output neuron.

  This output is the predicted probability of eventually winning from that position.

• Loss Function: The network uses mean squared error between the predicted value v_θ(s) and the final result z. After ~1 week training on 50 GPUs, the value network is strong enough to approximate a position's "worth" without playing the entire game out.

Putting Policies and Value Together: Monte Carlo Tree Search (MCTS)

Policy networks are great for suggesting strong moves, but alone they are imperfect. The value network can judge positions, but it's still not flawless. How do we combine them effectively during an actual game?

The Essence of MCTS

• Simulate: From the current board state, repeatedly simulate games to completion (using quick rollouts for depth).
• Prioritize: Among possible moves, focus more on those likely to yield good outcomes, but also explore untried possibilities.

Concretely, each MCTS iteration has four sub-steps:

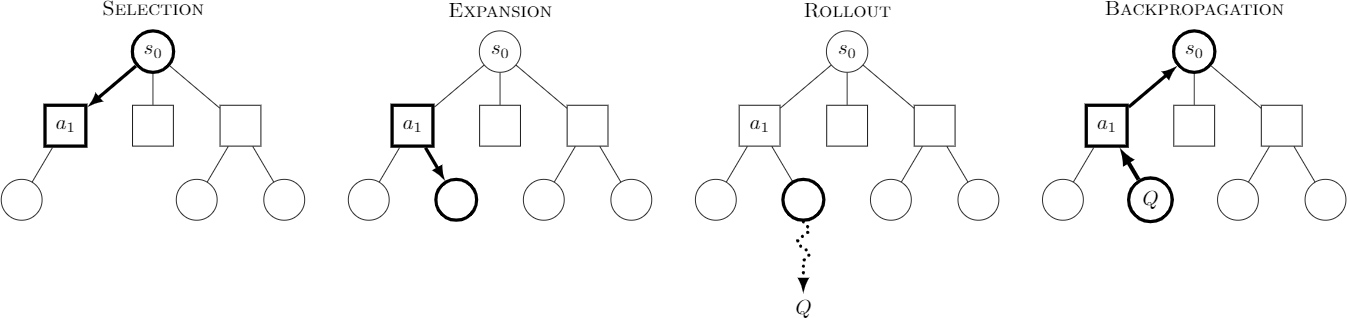
Image credit: Robert Moss via Wikipedia

• Selection

  Starting at the root (the current board position), choose moves along a path by maximizing: $Q(s,a) + u(s,a)$, where $Q$ is the average outcome so far, and $u$ encourages exploration for moves with high prior probabilities or fewer visits.

• Expansion

  Once you reach a leaf node (no further expansions), create children for new moves and initialize each edge with the SL policy's prior $P(s,a)$. The RL policy's top moves are good, but they can be narrower, so the SL policy (trained on a broad range of pro moves) is used here to encourage more diversity.

• Evaluation/Rollout

  From the new leaf, run the fast rollout policy ($\pi$) to the end of the game, or simply call the value network to get an estimate of how favorable that position is (or use both, depending on the variant).

• Backpropagation

  Update $Q(s,a)$ using the new outcome, increment the node visit counts, and adjust future selection accordingly.

Final Move Selection

After a large number of simulations (often thousands), AlphaGo picks its next move based on which child of the root was visited the most ($N(s,a)$ is highest). Empirically, the visit count is more stable than pure averages. Whichever move is visited the most is deemed the best balance of exploration and exploitation.

Hardware and Performance

AlphaGo's training and real-time execution can be computationally heavy. In the Lee Sedol match, AlphaGo ran on 1,920 CPUs and 280 GPUs (distributed across Google's data centers).

• SL Policy Training: 3 weeks on 50 GPUs to learn from 30 million expert moves.
• RL Policy: ~1 day on 50 GPUs (self-play).
• Value Network: ~1 week on 50 GPUs (collecting 30 million self-play games, each providing exactly one data point for training).

Even after this enormous process, AlphaGo still needs large clusters to handle real-time MCTS during a match, though future versions like AlphaGo Zero and AlphaZero have grown more efficient, sometimes running on only 4-8 TPUs.

Evolution: From AlphaGo to AlphaGo Zero to AlphaZero

The original AlphaGo uses human game data (supervised learning) as a bootstrap. But in AlphaGo Zero (2017), DeepMind removed that step entirely. AlphaGo Zero learned entirely from self-play, without any human game data, allowing it to explore and refine its own strategies from scratch, eventually surpassing the original AlphaGo 100-0. It combined the policy and value networks into a single architecture and was more computationally efficient. By removing reliance on human game records, it also developed innovative moves and strategies that humans had rarely or never seen.

After that, AlphaZero applied the same self-play approach to chess and shogi, reaching superhuman performance in each - underscoring the generality of the deep reinforcement learning + MCTS approach.

Conclusion: Why AlphaGo's Approach Works

AlphaGo's core insight was to use deep neural networks to capture both how professionals play (policy) and how to evaluate the likely winner of a position (value). It then integrated these learned networks into a tree search (MCTS) that drastically narrows down the vast search space. This synergy overcame the historical gap in computer Go and marked a turning point for AI research, showing that with enough data, computation, and the right architecture, systems can handle extremely complex tasks once deemed unattainable.

In essence, AlphaGo taught us that "intelligence" for certain narrow tasks is more accessible than once believed - given powerful function approximators, reinforcement learning, and the capacity to search effectively. While this success does not directly translate to every real-world problem, it reveals the potential for deep RL and search techniques to tackle domains of enormous complexity.

Further Reading

• D. Silver et al., "Mastering the game of Go with deep neural networks and tree search." Nature, 529, 484-489 (2016).
• D. Silver et al., "Mastering the game of Go without human knowledge." Nature, 550, 354-359 (2017).
• AlphaGo Documentary (2017), directed by Greg Kohs.